Concept of Algorithm
When we want to design and implement a program it is important to develop a "blueprint" of the program, which details the step by step procedure in arriving at the solution. This is just similar to creating an architectural plan for a house which we are planning to build. Such "blueprint" is called an algorithm.
The notation used for algorithm specification must conform to a basic set of criteria:
It must be concise - We must be able to describe the solution to a problem without writing multiple pages of text. It must be simple and short.
It must be unambiguous - The description of the procedure must not be open to alternative interpretations. We must remember that the algorithm will be executed by a machine which has no 'common sense' or inbuilt knowledge of the nature of the problem. It must be clear and precise.
It must be capable of machine execution - The actions described must be capable of translation into precise, machine-executable operations. This precludes such statements as "choose the best candidate". lf this were the object of the operation, the steps involved in evaluating the exact criteria for what constituted "best" must be clearly set out.
It must promote elegance in the solution - The tool must prevent the programmer from using practices at the design stage which Iead to poor programming style during implementation. The selection of an appropriate design tool has a great influence on the quality of the ultimate program. A good design tool will lead to programs which are elegant in their design, accurate rn their operation and easy to amend and enhance over a long period of time.
As natural languages do not bear the qualities mentioned above, following semi formal specifications and latterly even formal specifications were introduced.
Semi formal specifications - Flow charts, Pseudocode. Structured English, Decision tables, Decision trees, NS diagrams.etc.
Formal specifications - Z specifications, Algebra specifications, Pre and Post conditions, etc. These are based on pure mathematical methods.
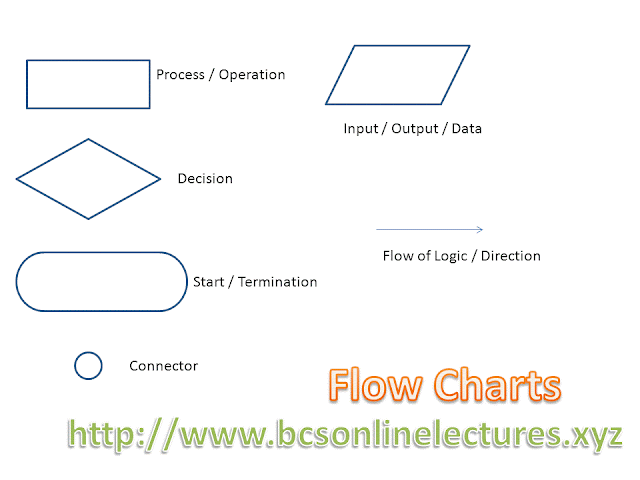
Flow Charts
A flowchart is a diagrammatic representation of the processes involved in arriving at a solution to a problem. While many symbols are included in its notation, the. Most important and most commonly used symbols are as follows;
It is important to understand the basic control constructs described below.
Sequence: In sequence processing, operation flows one after another.
- While Loop - Executes a set of operations repeatedly based on a given Boolean condition becomes true.
- Repeat / Until Loop - This is similar to while loop, but it compares the condition after executing a given set of operations.
- For Loop - This executes a given number of times, rather a condition becomes true or false.
Dry Running a Flow Chart
Dry running is step by step explanation of the process of a flow chart.
No comments:
Post a Comment